- In this algorithm we first find the smallest integer in the int array.
- Then we get the modulus for each element in the numbers of the array by dividing smallest integer and add all those modulus together.
- After processing each element in the array we check if the total of modulus is equals to 0. If it is equal to 0 then the GCD is current smallest value if that total is not equals 0 we deduct 1 from the previous smallest value and do the same computation.
- The algorithm will continue with the same operations until total of modulus becomes 0 or until smallest integer is 2.
- If there is any GCD, algorithm will return it or otherwise it will return -1.
See the following implementation of the algorithm.
public class GCD {
public static int findGcd(int... numbers) {
//Find the smallest integer in the number list
int smallest = numbers[0];
for (int i = 1; i < numbers.length; i++) {
if (numbers[i] < smallest) {
smallest = numbers[i];
}
}
//Find the GCD
while (smallest > 1) {
int counter = 0;
int modTot = 0;
while (counter < numbers.length) {
modTot += numbers[counter] % smallest;
counter++;
}
if (modTot == 0) {
//Return the gcd if any
return smallest;
}
//System.out.print(" "+ smallest);
smallest--;
}
//return -1 if there is no gcd
return -1;
}
public static void main(String[] x) {
System.out.println("The GCD of 15 18 42 108 : "+GCD.findGcd(new int[]{15, 18, 42,108}));
}
}
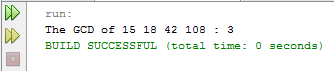
Here is the output for 15, 18, 42 and 108
Here is the output for 3,7 and 12